“Matrices” are a basic instrument for information science, machine studying, and linear algebra in Python. They retailer numbers in a grid-like construction and allow numerous operations corresponding to fixing equations and reworking information. Generally, we might have to reverse the impact of a matrix by discovering its inverse. Inverting a matrix may help us resolve a system of linear equations. To inverse a matrix, the “numpy” library is utilized in Python.
This text explains the right way to use “numpy” to inverse a matrix utilizing a number of examples.
What’s the Matrix Inverse?
Mathematically, a matrix is an array of rows and columns of num/numbers, symbols, or equations. Inverses of matrices are new matrices that produce the id matrix by multiplying them with the unique given matrices. A sq. matrix containing “ones” alongside the diagonal and “zeroes” elsewhere is the id matrix.
The way to Inverse a Matrix Using “numpy”?
The “numpy” library offers a easy perform known as “inv()” to invert a matrix. This perform takes a matrix as its enter and returns its inverse.
Syntax
Within the above syntax, the “a” parameter corresponds to the matrix to be inverted.
Be aware: The inverse of a matrix shouldn’t be relevant/purposeful to all varieties of matrices. It’s such that if the given matrix is singular, i.e., its determinant is “zero”, it doesn’t have an inverse. In such instances, the “inv()” perform will elevate a “LinAlgError” exception.
Instance 1: Computing Inverse of a “2×2” Matrix
Let’s take a easy “2×2” matrix and compute its inverse utilizing “numpy”:
import numpy
value_a = numpy.array([[52, 22], [43, 24]])
print(‘Given Matrix: n’,value_a)
inv_a = numpy.linalg.inv(value_a)
print(‘Inverse Matrix: n’,inv_a)
Within the above code, a “2×2” matrix is created and the “inv()” perform of the “numpy.linalg” module is used to compute its inverse.
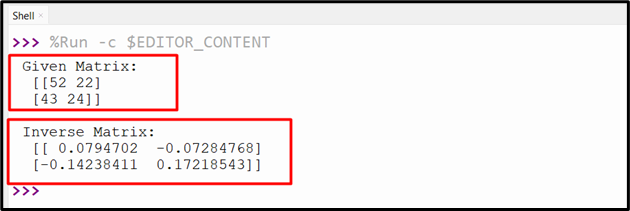
Output
The output snippet reveals the inverse matrix of the given matrix.
Instance 2: Computing Inverse of a “3×3” Matrix
Let’s take a “3×3” matrix and compute its inverse utilizing “numpy”:
import numpy
value_1 = numpy.array([[52, 32, 14], [24, 25, 36], [27, 28, 29]])
print(‘Given Matrix: n’,value_1)
inv_1 = numpy.linalg.inv(value_1)
print(‘nInverse Matrix: n’,inv_1)
The above code traces created a “3×3” matrix and computed its inverse through the “inv()” perform.
Output
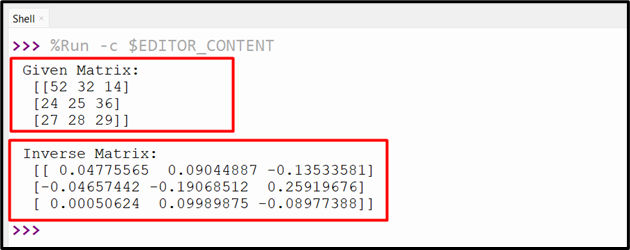
The above output returns the inverse of a “3×3” matrix.
Instance 3: Computing Inverse of “Singular Matrix”
Let’s take a singular matrix and attempt to compute its inverse:
import numpy
matrx_1 = numpy.array([[1, 2], [2, 4]])
inv_1 = numpy.linalg.inv(matrx_1)
print(inv_1)
Within the above code block, the “numpy.linalg.inv()” perform takes a singular matrix and returns the error “LinAlgError” upon calculating its inverse.
Output
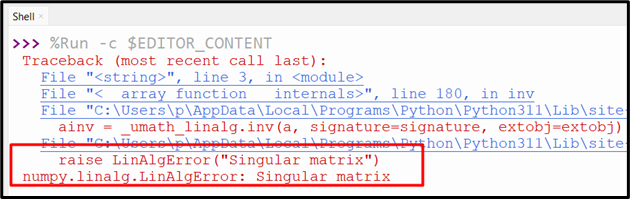
The above output implies that the inverse of the matrix has not been calculated because the given matrix is singular.
Various Method: Discover the Inverse of a Matrix Utilizing the “scipy” Library
The “linalg.inv()” perform of the “scipy” library can be used to seek out the numpy inverse. Let’s perceive it through the under instance.
Instance
The next code makes use of the “linalg.inv()” perform of the “scipy” library to get the inverse of the matrix:
import numpy
from scipy import linalg
value_a = numpy.matrix([[27, 32,],[43, –25]])
print(‘Given Matrix: n’,value_a)
value_b = linalg.inv(value_a)
print(‘nInverse Matrix: n’,value_b)
On this code, the “linalg.inv()” perform of the “numpy” library is used to seek out the inverse of the desired matrix.
Output
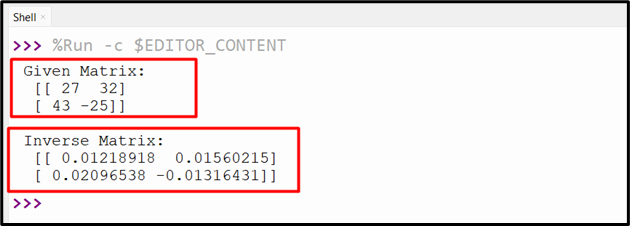
This end result returns the inverse matrix of the given matrix.
Conclusion
Matrix inversion is an important frequent operation in linear algebra, and “numpy” affords a easy perform “inv()” for this goal. This text mentioned the right way to inverse a matrix with “numpy” utilizing the “inv()” perform. The “scipy” library contains a perform named “linalg.inv()” that will also be used to seek out the inverse of the given matrix. Numerous examples of discovering the inverse of matrices are demonstrated with completely different sizes, together with a singular matrix.
